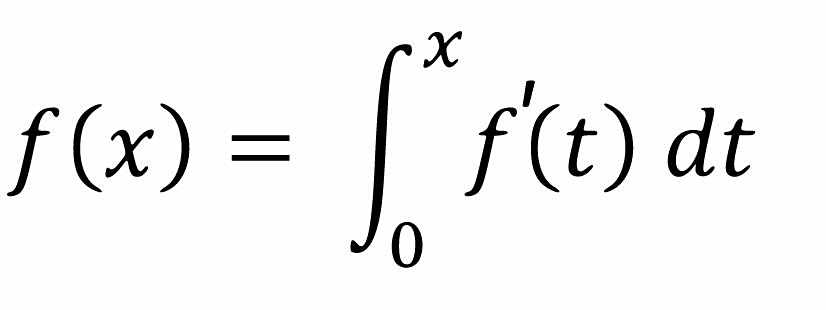反函数的定义

在数学里，反函数，也称为逆函数（Inverse function），为对一个定函数做逆运算的函数。[1]

什么是逆？我们知道减法是加法的逆运算，除法是乘法的逆运算，比如

1+2=31 + 2 = 3

其中，11 是起始值，对其进行加 22 运算得到结果 33

反之，如果执行这个操作的逆，即

3−2=13 - 2 = 1

那么就能够得到原来的起始值

而在这个逆运算中，33 是起始值，11 是结果

因此，一个逆的结果是原来的起始值，逆的起始值是原来的结果

将这个概念推广到函数，我们有反函数的概念

设函数 f:D→f(D)f:D\rightarrow f(D) 是单射，则它存在逆映射 f−1:f(D)→Df^{-1}:f(D)\rightarrow D，称此映射 f−1f^{-1} 为函数 ff 的反函数，函数 ff 称为反函数 f−1f^{-1} 的直接函数 [2]

由这个定义可以直到，当将一个数 xx 输入 ff 得到 yy 时，那么将 yy 输入 f−1f^{-1} 就能得到 xx

而 ff 是 D→f(D)D\rightarrow f(D) 的映射，即像所在的集合就是函数的值域 f(D)f(D)，因此 ff 也是一个满射

从而，f:A→Bf:A\rightarrow B 的反函数存在的充要条件是 ff 是数集 AA 到数集 BB 的双射，简化来看，即

函数 f:D→f(D)f:D\rightarrow f(D) 存在的反函数的充要条件是 ff 是从定义域 DD 到其值域 f(D)f(D) 的 单射

此外，由于严格单调的函数一定满足单射，因此有

严格单调的函数一定存在反函数

反之，如果一个函数存在反函数，却不一定是严格单调的

为什么会在主观上认为单调和单射等价：如果函数不单调，那么函数图像一定会“拐弯”，根据介值定理，对于同一个 yy 值，可能就会对应多个 xx 值，导致反函数称为多值函数，这不在我们讨论范围内

又因为介值定理的一个前提是函数必须是连续的，因此，我们可以得到

连续函数具有反函数的充要条件是它是严格单调的

如何求一个函数的反函数？

举个例子，假设有函数 f(x)=2x+1f(x) = 2x + 1

这个函数关系表示了一个已知 xx，求函数值即 yy 的过程，而反函数则表示已知 yy，求 xx 的过程

因此可以得到 x=y−12x = \dfrac{y - 1}{2}，也即函数 ff 的反函数 f−1f^{-1} 可以表示为 f−1(y)=y−12f^{-1}(y) = \dfrac{y - 1}{2}

在这里，反函数 f−1f^{-1} 中的 yy 表示函数值 xx 随 yy 的变化而变化，而 xx 和 yy 对应的表达式和原来的 ff 还是相同的，因此 ff 和 f−1f^{-1} 在同一个坐标系 xOyxOy 中画出来的图像也是相同的

但是，我们常把 xx 看作因变量，所以 ff 的反函数 f−1f^{-1} 一般写作 f−1(x)=x−12f^{-1}(x) = \dfrac{x - 1}{2}，即把 xx 轴和 yy 轴互换了

因此，函数 f(x,y)=0f(x, y) = 0 的表达式其实也是 f−1(x,y)=0f^{-1}(x, y) = 0 的表达式，但是因为习惯问题，反函数一般写成 f−1(y,x)=0f^{-1}(y, x) = 0

反函数的性质

定义域和值域：f−1f^{-1} 的定义域是 ff 的值域，f−1f^{-1} 的值域是 ff 的定义域

互逆性：若 f(a)=bf(a) = b，则 f−1(b)=af^{-1}(b) = a，即 f−1(f(x))=xf^{-1}(f(x)) = x（f(f−1(y))=yf(f^{-1}(y)) = y 也成立）

Problem 1 设函数 f(x)f(x) 在 (0,+∞)(0, +\infty) 内为单调可导函数，它的反函数为 f−1(x)f^{-1}(x)，且 f(x)f(x) 满足等式 ∫1f(x)f−1(t)dt=x43−16\displaystyle\int^{f(x)}_{1}f^{-1}(t)\mathrm{d}t= x^{\frac{4}{3}} - 16，则 f(x)f(x) 的表达式为

题目给出函数 f(x)f(x) 单调可导，因此 f(x)f(x) 单调连续，故其反函数是存在的

根据积分式，我们可以知道 x=f−1(t)x = f^{-1}(t) 是 tt 的反函数，因此有 t=f(x)t = f(x)

作换元 t=f(x)t = f(x)，积分上下限分别变为 xx 和 88（带入 t=f(x)=1t = f(x) = 1 即可求得），因此

∫8xxd(f(x))=x43−16\int_{8}^{x}x\mathrm{d}(f(x)) = x^{\frac{4}{3}} - 16

分部积分得

xf(x)∣8x−∫8xf(x)dx=x43−16xf(x)\mid_{8}^{x} - \int_{8}^{x}f(x)\mathrm{d}x = x^{\frac{4}{3}} - 16

两边求导得

xf′(x)=43x13xf'(x) = \dfrac{4}{3}x^{\frac{1}{3}}

解微分方程得 f(x)=4x13+Cf(x) = 4x^{\frac{1}{3}} + C，带入 f(8)=1f(8) = 1 得 C=−7C = -7，从而

f(x)=4x13−7f(x) = 4x^{\frac{1}{3}} - 7

实际上，直接对等式两边求导 ∫1f(x)f−1(t)dt=x43−16\displaystyle\int^{f(x)}_{1}f^{-1}(t)\mathrm{d}t= x^{\frac{4}{3}} - 16 即可得到

f−1(f(x))⋅f′(x)=43x13f^{-1}(f(x))\cdot f'(x) = \frac{4}{3}x^{\frac{1}{3}}

再利用互逆性 f−1(f(x))=xf^{-1}(f(x)) = x 即可解决

对称性：函数 y=f(x)y = f(x) 的图像与反函数 y=f−1(x)y = f^{-1}(x) 的图像关于直线 y=xy = x 成轴对称

即如果点 (a,b)(a, b) 在 ff 的图像上，那么点 (b,a)(b, a) 必然在 f−1f^{-1} 的图像上

Problem 2 若 x1x_1 是方程 xex=e2xe^x=e^2 的解，x2x_2 是方程 xln⁡x=e2x\ln x=e^2 的解，求 x1⋅x2x_1\cdot x_2 的值

由题可知 ex1=e2x1e^{x_1} = \dfrac{e^2}{x_1}，ln⁡x2=e2x2\ln x_2 = \dfrac{e^2}{x_2}

显然 y=exy = e^x 和 y=ln⁡xy = \ln x 互为反函数，故 y=exy = e^x 和 y=ln⁡xy = \ln x 关于 y=xy = x 对称

显然，y=e2xy = \dfrac{e^2}{x} 也关于 y=xy = x 对称

设 y=exy = e^x 与 y=e2xy = \dfrac{e^2}{x} 的交点为 A(x1,e2x1)A\left(x_1, \dfrac{e^2}{x_1}\right)，y=ln⁡xy = \ln x 与 y=e2xy = \dfrac{e^2}{x} 的交点为 B(x2,e2x2)B\left(x_2, \dfrac{e^2}{x_2}\right)

根据对称性，有

{x1=e2x2e2x1=x2\begin{cases} x_1 = \dfrac{e^2}{x_2}\\ \dfrac{e^2}{x_1} = x_2 \end{cases}

因此 x1x2=e2x_1x_2 = e^2

单调性：反函数 f−1(x)f^{-1}(x) 与其直接函数 f(x)f(x) 的单调性一致

奇偶性：如果 f(x)f(x) 是奇函数且存在反函数，那么 f−1(x)f^{-1}(x) 也是奇函数

反函数的导数

如果函数 x=f(y)x = f(y) 在区间 IyI_y 内单调可导，且 f′(y)≠0f'(y) \neq 0，那么它的反函数 y=f−1(x)y = f^{-1}(x) 在区间 Ix={x∣x=f(y),y∈Iy}I_x = \{x\mid x=f(y), y\in I_{y}\} 内也可导，且 [2:1]

[f−1(x)]′=1f′(y)或dydx=1dxdy[f^{-1}(x)]' = \frac{1}{f'(y)} \text{或} \frac{\mathrm{d}y}{\mathrm{d}x} = \dfrac{1}{\dfrac{\mathrm{d}x}{\mathrm{d}y}}

证明 题目给出 x=f(y)x = f(y) 在区间 IyI_y 内单调可导，说明 x=f(y)x = f(y) 连续且单调，故其反函数 y=f−1(x)y = f_{-1}(x) 存在

任取 x∈Ixx\in I_x，有增量 Δx\Delta x（ Δx≠0\Delta x\neq 0 且 x+Δx∈Ixx+\Delta x \in I_x ），由 f−1(x)f^{-1}(x) 的单调性可知

Δy=f−1(x+Δx)−f−1(x)≠0\Delta y = f^{-1}(x + \Delta x) - f^{-1}(x) \neq 0

又 y=f−1(x)y = f^{-1}(x) 连续，则

lim⁡Δx→0Δy=0\lim_{\Delta x\to 0}\Delta y = 0

因此

[f−1(x)]′=lim⁡Δx→0ΔyΔx=lim⁡Δx→01ΔxΔy=lim⁡Δy→01ΔxΔy=1f′(y)[f^{-1}(x)]' = \lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0}\frac{1}{\frac{\Delta x}{\Delta y}} = \lim_{\Delta y \to 0}\frac{1}{\frac{\Delta x}{\Delta y}} = \frac{1}{f'(y)}

Problem 3 设函数 f(x)f(x) 单调可导，φ(x)\varphi(x) 是 f(x)f(x) 的反函数，且 f(2)=4f(2) = 4, f′(2)=5f'(2) = \sqrt{5}，求 φ′(4)\varphi'(4) 的值

根据函数 f(x)f(x) 的单调性，当 f(x)=4f(x) = 4 时，x=2x = 2，因此直接套用反函数求导公式可得

φ′(4)=1f′(2)=15\varphi'(4) = \frac{1}{f'(2)} = \frac{1}{\sqrt{5}}

这里可能会容易搞混 xx 和 yy，实际上，只要推一遍反函数求导公式就清晰的多

φ′(4)=lim⁡Δx→0φ(4+Δx)−φ(4)Δx\varphi'(4) = \lim_{\Delta x \to 0}\frac{\varphi(4 + \Delta x) - \varphi(4)}{\Delta x}

设 y1=φ(4+Δx)y_1 = \varphi(4 + \Delta x)，y2=φ(4)y_2 = \varphi(4)，则 4+Δx=f(y1)4 + \Delta x = f(y_1)，4=f(y2)⇒y2=24 = f(y_2)\Rightarrow y_2 = 2，则

φ′(4)=lim⁡y1→y2y1−y2f(y1)−f(y2)=1lim⁡y1→y2f(y1)−f(y2)y1−y2=1f′(y2)=15\varphi'(4) = \lim_{y_1\to y_2}\frac{y_1 - y_2}{f(y_1) - f(y_2)} = \frac{1}{\displaystyle\lim_{y_1\to y_2}\frac{f(y_1) - f(y_2)}{y_1 - y_2}} = \frac{1}{f'(y_2)} = \frac{1}{\sqrt{5}}

下面来推导反函数的二阶导数公式

前面我们知道 [f−1(x)]′=1f(y)[f^{-1}(x)]' = \dfrac{1}{f(y)}，那么 [f−1(x)]′′[f^{-1}(x)]'' 的计算过程如下

[f−1(x)]′′=ddx(1f′(y))[f^{-1}(x)]'' = \frac{\mathrm{d}}{\mathrm{d}x}\left(\dfrac{1}{f'(y)}\right)

由链式法则得

ddx(1f′(y))=ddy(1f′(y))dydx=ddy(1f′(y))1dxdy\frac{\mathrm{d}}{\mathrm{d}x}\left(\dfrac{1}{f'(y)}\right) = \frac{\mathrm{d}}{\mathrm{d}y}\left(\dfrac{1}{f'(y)}\right)\frac{\mathrm{d}y}{\mathrm{d}x} = \frac{\mathrm{d}}{\mathrm{d}y}\left(\dfrac{1}{f'(y)}\right)\frac{1}{\frac{\mathrm{d}x}{\mathrm{d}y}}

因此

[f−1(x)]′′=−f′′(y)[f′(y)]3\textcolor{red}{[f^{-1}(x)]'' = -\frac{f''(y)}{[f'(y)]^3}}

Problem 4 已知函数 f(x)f(x)，φ(x)\varphi(x) 是 f(x)f(x) 的反函数，f(x)f(x) 可导且 f′(x)=ex2+x+1f'(x) = e^{x^2+x+1}，f(0)=3f(0) = 3，求 φ′′(3)\varphi''(3)

由于函数 f(x)f(x) 可导，因此 f(x)f(x) 连续，又 f(x)f(x) 存在反函数，因此 f(x)f(x) 单调

所以当 f(x)=3f(x) = 3 时，x=0x = 0

又反函数的二阶导数公式可得

φ′′(3)=−f′′(0)[f′(0)]3=−1e2\varphi''(3) = -\frac{f''(0)}{[f'(0)]^3} = -\frac{1}{e^2}

反三角函数初探

反三角函数的定义

三角函数显然不满足单射，但是在特定区间中，我们可以使三角函数满足单射，比如当 x∈(−π2,π2)x\in\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right) 时，y=sin⁡xy=\sin x 满足单射，因此它有反函数 y=arcsin⁡xy = \arcsin x，据此，我们可以定义六个三角函数的反三角函数如下

函数名称 符号表示 定义域 (xx) 值域 (主值区间) 备注
反正弦 y=arcsin⁡xy = \arcsin x [−1,1][-1, 1] [−π2,π2]\left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right] 单调递增，奇函数
反余弦 y=arccos⁡xy = \arccos x [−1,1][-1, 1] [0,π][0, \pi] 单调递减，非奇非偶
反正切 y=arctan⁡xy = \arctan x (−∞,+∞)(-\infty, +\infty) (−π2,π2)\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right) 单调递增，奇函数，有两条水平渐近线 y=±π2y=\pm \dfrac{\pi}{2}
反余切 y=arccot xy = \text{arccot } x (−∞,+∞)(-\infty, +\infty) (0,π)(0, \pi) 单调递减，非奇非偶，有两条水平渐近线 y=0,y=πy=0, y=\pi
反正割 y=arcsec xy = \text{arcsec } x (−∞,−1]∪[1,+∞)(-\infty, -1] \cup [1, +\infty) [0,π],y≠π2[0, \pi], y \neq \dfrac{\pi}{2} 在两段区间上单调递增，排除 y=π2y=\dfrac{\pi}{2}
反余割 y=arccsc xy = \text{arccsc } x (−∞,−1]∪[1,+∞)(-\infty, -1] \cup [1, +\infty) [−π2,π2],y≠0\left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right], y \neq 0 在两段区间上单调递减，排除 y=0y=0

反三角函数的导数

比如求反三角函数 y=arcsin⁡xy = \arcsin x 的导数，套用反函数的求导公式得

(arcsin⁡x)′=1sin⁡′y=11−x2(\arcsin x)' = \frac{1}{\sin'y} = \frac{1}{\sqrt{1 - x^2}}

实际上，由于 x=sin⁡yx = \sin y，利用隐函数求导法则可得

1=y′cos⁡y1 = y'\cos y

从而

y′=1cos⁡y=11−x2y' = \frac{1}{\cos y} = \frac{1}{\sqrt{1 - x^2}}

同样的，就能得到其余反三角函数的导数如下

函数 yy 导数 y′y' 成立条件
arcsin⁡x\arcsin x 11−x2\dfrac{1}{\sqrt{1-x^2}} ∣x∣<1|x| < 1
arccos⁡x\arccos x −11−x2-\dfrac{1}{\sqrt{1-x^2}} ∣x∣<1|x| < 1
arctan⁡x\arctan x 11+x2\dfrac{1}{1+x^2} x∈Rx \in \R
arccot x\text{arccot } x −11+x2-\dfrac{1}{1+x^2} x∈Rx \in \R
arcsec x\text{arcsec } x 1∣x∣x2−1\dfrac{1}{|x|\sqrt{x^2-1}} ∣x∣>1|x| > 1
arccsc x\text{arccsc } x −1∣x∣x2−1-\dfrac{1}{|x|\sqrt{x^2-1}} ∣x∣>1|x| > 1

  1. Wikipedia - 反函数 ↩︎

  2. 同济版高等数学（第八版 上册） ↩︎ ↩︎